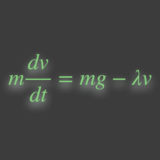振動現象のうち、質点に速度に比例した抵抗力がかかる「減衰振動」について扱います。まず初めに自分で運動方程式を間違えなく書き下せるように力の向きと符号の確認をします。そして、具体的に解く前に、エネルギー収支をみて物理的な考察をしてみます。その上で実際に解を求めます。
さらに、問題の例を通してより強い解の仮定をして一般解を求めて、全体をまとめます。最後に各節でのまとめを再掲しているので、復習の際はこちらを眺めると良いと思います。
慣性抵抗に関する記事も書きました↓
慣性抵抗の問題を解いてみる
目次
運動方程式を立てて、定性的に理解する
バネに繋がれていて、水平方向に運動する質点の単振動現象を扱う際には、理想化して考えるために色々な効果を無視しています。例えば「空気抵抗」や地面から受ける「摩擦」、「バネの歪み・バネの非線形性」などがあります。少しずつ、効果の大きそうなものから考慮して運動を考えてみることにします。ここでは速度の１乗に比例する「粘性抵抗」について考えてみます。実験のセットアップを下の図に描きました。
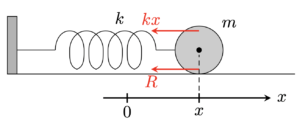
質点にかかる力の大きさを図に赤色で表現してみました。復元力を$kx$、速さに比例した抵抗力を$R$としました。どちらも力の大きさですので、後で力の働く向きについても考えます。抵抗力の表し方については、参照するテキストによって様々な表現がありますが、速度に比例していることを強調すれば速さを$v=\dot{x}$として、$\lambda{\dot{x}}$とも書けますし、後に運動方程式を楽に解く(式の質量の項$m$などを消す)ことを見越して、$2m\gamma\dot{x}$と書いたりします。(このとき、$\gamma$は$\rm{s}^{-1}$の次元になります。) まとめると、質点に作用する速さに比例する抵抗力の大きさは、$$R=\lambda{\dot{x}}=2m\gamma\dot{x}$$と書けます。(ここで「ドット」は時間の微分を表しています。)
次に、運動方程式を立てるために、力の向きを考えてみます。今、図に書き入れた$x$軸は右向きが正の値となっています。これに合わせて、右向きの力なら正の値で、左向きの力なら負の値で表現することになります。復元力は向き付きで、もちろん$-kx$です。
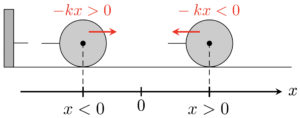
一応向きの確認をしておくと、バネの自然長を$x=0$とすれば、$x>0$のときは$-kx<0$で左向きの縮む力、$x<0$のときは$-kx>0$で右向きの伸びる力が働いています。
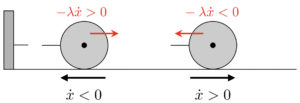
速度に比例した抵抗力は、正の方向に移動しているとき、すなわち速度が$\dot{x}>0$のときには左向きの力$-\lambda\dot{x}<0$を、負の方向に移動しているとき、すなわち$\dot{x}<0$のときには右向きの力$-\lambda\dot{x}>0$を受ければよく、結局、速度に比例する抵抗力は、移動する向きに関わらず統一的に$-\lambda\dot{x}$と書けば良いと分かります。この抵抗力が、床から受ける摩擦だった場合の話はまた別で、右向きの運動なら$-\mu{mg}$、左向きの運動なら$+\mu{mg}$として、運動している方向によって運動方程式を別々に書く必要があるので注意です。
力の書き下し方について色々と述べてきましたが、ここを間違えると一巻の終わりですので、注意して立てると良いです。結局、運動方程式は$$m\ddot{x}=-kx-\lambda{\dot{x}}\ \ \cdots(*)$$となります。ここで一旦立ち止まって、運動の解$x(t)$を求める前に、大雑把に、定性的に運動を考えてみます。この運動の身近な例としては$RLC$回路でしょうか。そんなわけない(？)ですかね、日常生活の範囲で想像できるのは、振り子を壁に当てながら振動させる現象です。壁が比較的ツルツルなら振幅がゆっくりと減衰しながら振動することが想像できますし、壁がゴツゴツなら抵抗力が強すぎて振動する間も無くすぐに減衰して止まるでしょう。このうち前者を、減衰しながらの振動という意味で「減衰振動(damped oscillation)・不足減衰」、後者を過剰な・オーバーな減衰という意味で「過減衰(over damping)」と言います。また、両者のちょうど境目に相当する振動を「臨界減衰(critical damping)」と言います。
バネ(自然長: $x=0$)に繋がれて振動している物体に、速度$\dot{x}$に比例した粘性抵抗が働いているときの運動方程式は、
$$m\ddot{x}=-kx-\lambda\dot{x}$$
であり、抵抗成分が微小であれば「減衰振動・不足減衰」、抵抗成分が強ければ「過減衰」、これらの境界が「臨界減衰」となる。
少し余談ですが、実際に上に書いたようなバネ・質点系の実験装置を組み立てようとするのは難しいです。ホームセンターに遊びに行ってバネを買うのですが、現実のバネは「押しバネ」と「引きバネ」に分けられているのが主流らしく、復元力として両方の性質を持ったバネを入手することはできませんでした。良いバネが見つけられたら実験動画を撮ろうと思います。
エネルギーの出入り(収支)について
実際に解く前にすぐにわかる物理的な考察として、エネルギーの保存について考えてみます。運動方程式は、運動量$mv$という注目すべき量が外界からの作用$f$で変化するという形の式でした。すなわち式で書くなら、$$\frac{d}{dt}(mv)=f$$です。この左辺は時間微分なので運動量$mv$の時間変化であり、それは右辺の力によって起こされるわけです。特にこの右辺を、注目している系に変化を及ぼす源という意味でsource termと言ったりもします。
$$f^{\prime}(t)>0\Rightarrow{}f(t+\Delta{t})>f(t)$$であり、微分係数が正のとき、関数$f(t)$は増加します。ここで、$f(t)=mv(t)$とおけば、それは運動量であり、その時間的な変化は力$f$によって決まるというのが運動方程式の意味しているところです。
では、これと同じ形の、「”何か”の時間変化が外界からの作用で生じる」という式を新たに探してみたいのですが、ここでは運動方程式$(*)$の両辺に$\dot{x}$を内積してみましょう。$$m\dot{x}\ddot{x}=-kx\dot{x}-\lambda({\dot{x}})^2$$ドットの表記をやめて(ラグランジュ記法に変えて)、左辺は$\dot{x}=v$とすると、$$mv\frac{dv}{dt}=-kx\frac{dx}{dt}-\lambda({\dot{x}})^2\ \ \cdots(A)$$となります。ここで、運動エネルギー$ \dfrac{1}{2}m\{v(t)\}^2 $と弾性エネルギー$ \dfrac{1}{2}kx(t)^2 $をそれぞれ時間$t$で微分すると、合成関数の微分を使って、$$\frac{d}{dt}\bigg(\frac{1}{2}mv(t)^2\bigg)=\frac{d}{dv}\bigg(\frac{1}{2}mv(t)^2\bigg)\frac{dv}{dt}=mv(t)\frac{dv}{dt}$$ $$\frac{d}{dt}\bigg(\frac{1}{2}kx(t)^2\bigg)=\frac{d}{dx}\bigg(\frac{1}{2}kx(t)^2\bigg)\frac{dx}{dt}=kx(t)\frac{dv}{dt}$$という形になります。一番右の式の形が先程の式$(A)$に現れているので、この合成関数の微分を右から左へ辿れば、「”何か”(ここでは運動エネルギーと弾性エネルギーの和)の時間変化」を式に顕に書くことができます。結局、式$(A)$を書き換えると次のようになります。
$$\frac{d}{dt}\bigg(\frac{1}{2}mv^2+\frac{1}{2}kx^2\bigg)=-\lambda(\dot{x})^2$$
大きい丸括弧の中は、運動エネルギーと弾性エネルギーの和なので、この系の力学的エネルギーになっています。それに$ \dfrac{d}{dt} $が付いているため、左辺は「力学的エネルギーの変化」を表しています。その変化を起こす原因である右辺は「抵抗の(単位時間あたりの)仕事」を表しています。ここで右辺は２乗が入っていることから全体で必ずマイナスの値なので、それと＝で結ばれている左辺は必ずマイナスであり、系の力学的エネルギーはどんどんと抵抗量の仕事によって散失していくことが読み取れます。
なお、減衰に寄与する成分がなければ($\lambda=0$なら)上の式は、
$$\frac{d}{dt}\bigg(\frac{1}{2}mv^2+\frac{1}{2}kx^2\bigg)=0$$
となり、カッコ内を時間で微分したら$0$となっているので、カッコ内は定数だと分かります。つまり、定数$E$を使って
$$\frac{1}{2}mv^2+\frac{1}{2}kx^2=E$$
の力学的エネルギーの保存が導かれます。
運動方程式 $m\ddot{x}=-kx-\lambda{\dot{x}}$ の両辺に速度 $v=\dot{x}$ を内積すると、$$mv\frac{dv}{dt}=-kx\frac{dx}{dt}-\lambda({\dot{x}})^2\ \ \cdots(A)$$となり、加速度由来の項は運動エネルギーの時間変化、復元力由来の項は弾性エネルギーの時間変化へ書き換えられるので、結局、運動方程式から$$\frac{d}{dt}\bigg(\frac{1}{2}mv^2+\frac{1}{2}kx^2\bigg)=-\lambda(\dot{x})^2$$が導ける。この式を見れば、力学的エネルギーが抵抗力の仕事により散失していくことがわかる。
運動方程式に解を仮定して代入する
起こる現象のおおよその検討がついたところで、実際に解を求めてみます。運動方程式は、
$$m\ddot{x}=-kx-\lambda{\dot{x}}\ \ \cdots(*)$$であり、抵抗力の比例係数$\lambda$を、式を綺麗にするために$\lambda=2m\gamma$と置き換えると、$$m\ddot{x}=-kx-(2m\gamma){\dot{x}}$$ここで、「$2$」を付けたのは、結局後で２次方程式に帰着させるので解くのが楽になるためです。両辺を$m$で割って、式を左辺に寄せ集めると、$$\ddot{x}+2\gamma\dot{x}+\frac{k}{m}x=0$$となります。この式において、$\gamma=0$ (抵抗なし)とすると、角振動数 $\omega_0=\sqrt{k/m}$の単振動の運動方程式になります。この$\omega_0$を使って書き換えると、$$\ddot{x}+2\gamma\dot{x}+\omega_0^2x=0$$となります。この微分方程式は２階の方程式なので、一般解を求めるために、２つの一次独立な解を探す必要があります。(詳しくは→「初めての微分方程式」)
この微分方程式の$ x $に代入して成立する解を求めれば良いのですが、ここでは指数関数の形の解:$$x(t)=e^{\alpha{t}}$$を想定してみます。この想定が正しければ、２つ$e^{\alpha{t}}$の定数倍の足し合わせで全ての解を表現することができます。実際に式へ代入すると、$$(\alpha^2+2\gamma\alpha+\omega_0^2)e^{\alpha{t}}=0$$となります。このとき、別な関数を仮定していたらここの代入が大変になって、その上$e^{\alpha{t}}$で括ることはできない面倒さが生じます。まずはよくわからない微分方程式の解を探る上で、微分が楽なやり方で探してみる、というのがここで解を指数関数だと仮定した１つのモチベーションです。一度この解き方を経験しておくと、実は解はもう少し詳しく予想できます。そのやり方で解くともっと楽に、統一的にできます。(この記事の最後の方で例題として扱いました。)別なアプローチとしては、↓のような記事もあります。
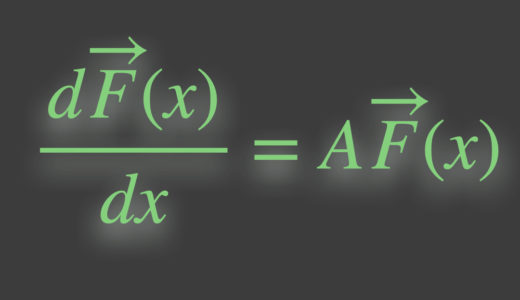線形微分方程式で解をe^x(exp)と仮定するのはなぜか？
ここで、$e^{\alpha{t}}=0$はこの方程式を満たしますが、それだと$x(t)=0$となり、原点(バネの自然長)で止まっているだけで何からも力を受けないというクソつまらない解が出て来るので、ここでは$e^{\alpha{t}}\neq0$として解きましょう。従って、$$\alpha^2+2\gamma\alpha+\omega_0^2=0$$となり、これは$\alpha$が複素数の範囲で必ず２つの解が存在するので、当初の目的だった、２つの独立な解が求められそうです。解の公式から、$$\alpha=-\gamma\pm\sqrt{\gamma^2-{\omega_0}^2}$$と求まります。ここで、この$\alpha$が実数なのか、複素数なのか考えるのは非常に重要です。今は、解を$$x(t)=e^{\alpha{t}}$$と仮定しているため、$\alpha$が実数となる、$\gamma>\omega_0$の場合には、(これは抵抗由来の文字である$\gamma$が振動の成分$\omega_0$よりも大きい場合。)$$\alpha=-\gamma\pm(\gamma\text{より小さい正の数})<0$$となるため、どちらの解も$e$のマイナス乗となり、急速に減衰していく、振動しない解になります。これは「過減衰」に対応します。一方、$\gamma<\omega_0$の場合、(これは先程とは逆で、振動成分$\omega_0$が抵抗成分$\gamma$よりも大きい場合。)ルートの中身が負の数になるため、$$\omega_1=\sqrt{\omega_0^2-\gamma^2}$$と置き直すと、$$\alpha=-\gamma\pm{i}\omega_1$$となり、今度は解が$e$の複素数乗となるので、振動する解になります。(指数関数と三角関数は親戚関係みたいなもので、$e^{i\theta}=\cos\theta+i\sin\theta$という等式で、指数の肩に複素数を乗せると三角関数になります。) こちらが、「減衰振動」に対応します。ここら辺で一旦まとめましょう。
運動方程式$ m\ddot{x}=-kx-\lambda{\dot{x}} $において、抵抗成分を$\lambda=2m\gamma$、(抵抗がない場合の)角振動数を$\omega_0=\sqrt{k/m}$とおくと、$$\ddot{x}+2\gamma\dot{x}+{\omega_0}^2x=0$$のようにまとめられる。ここで、解を$$x(t)=e^{\alpha{t}}$$と仮定して代入すれば、$e^{\alpha{t}}\neq0$として、$$\alpha^2+2\gamma\alpha+\omega_0^2=0$$より、$$\alpha=-\gamma\pm\sqrt{\gamma^2-{\omega_0}^2}$$ここで、$\gamma>\omega_0$の場合(過減衰)には、$\alpha$が負の実数となるために、急速に減衰していく振動しない解が得られ、一方、$\gamma<\omega_0$の場合(減衰振動)には、$\alpha$が複素数$-\gamma\pm{i}\omega_1$になるため、振動する解が得られる。
減衰振動・臨界減衰・過減衰の具体的な解の形は？グラフの概形は？
抵抗$\gamma$と単振動の角振動数$\omega_0$の大小関係で、３つの場合に分けて考えます。
減衰振動 ($\gamma<\omega_0$ の場合)
抵抗が弱い場合、振動する解が得られるのでした。具体的には、$$\alpha=-\gamma\pm\sqrt{\gamma^2-{\omega_0}^2}$$のルートの中身が負の値になるので、置き換えを $\omega_1=\sqrt{\omega_0^2-\gamma^2}$ として、$$\alpha=-\gamma\pm{i}\omega_1$$とします。一般解は独立な２つの解を一次結合すればいいので、任意定数$C_1,C_2$として$$x(t)=C_1e^{(-\gamma+i\omega_1)t}+C_2e^{(-\gamma-i\omega_1)t}$$ここで、共通する実数乗$e^{-\gamma{t}}$をまとめれば、$$x(t)=e^{-\gamma{t}}(C_1e^{i\omega_1{t}}+C_2e^{-i\omega_1{t}})$$となり、丸括弧内が三角関数になるので(詳しくは$x$が実数の条件から、$B$が$A$の複素共役になることを使います。) 結局、任意定数$C_1^{\prime},C_2^{\prime}$として$$x(t)=e^{-\gamma{t}}\{C_1^{\prime}\cos(\omega_1{t})+C_2^{\prime}\sin(\omega_1{t})\}$$となります。グラフを描くとこんな感じです。$\gamma$と$\omega_0$の比率によって色々と描画してみました。
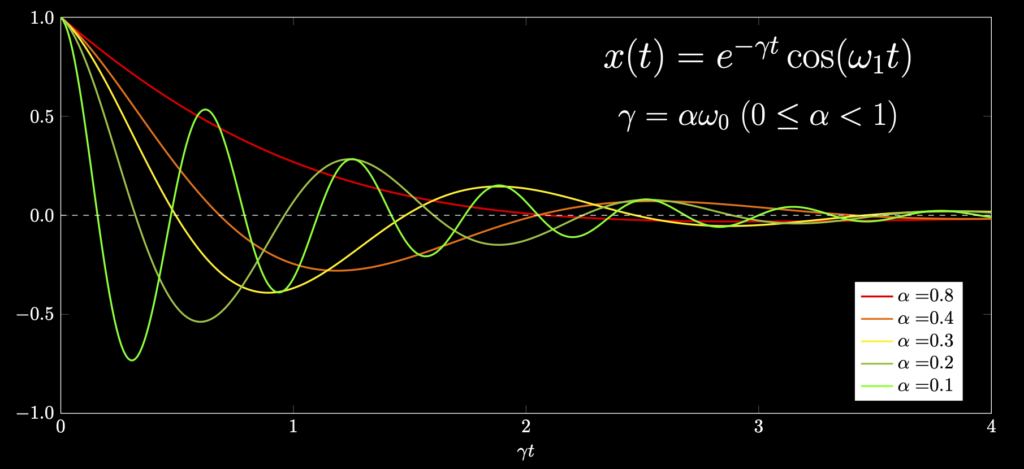
ここで、抵抗を$\gamma=0$として無くすと、単振動の一般解と同じ形をしています。しかしながら、角振動数は違う値になっていることに注意です。置き直した角振動数は、$$\omega_1=\sqrt{\omega_0^2-\gamma^2}<\omega_0$$であり、抵抗がない場合の振動と比べて、抵抗$\gamma$が大きいほど、角振動数は減少します。周期で考えると、$T=2\pi/\omega$なので、周期は長くなります。ところで、抵抗$\gamma$の出どころは$2m\gamma\dot{x}$と置いた抵抗力で、これが力の次元$\rm{N}=\rm{kg\cdot{m}s^{-2}}$を持つため、$\gamma$は$\rm{s^{-1}}$で角振動数と同じ次元になっています。だからこそ、角振動数$\omega$との引き算ができて、また、指数の肩の上には無次元の数値が乗っかりますが、ちょうど今の場合$e^{-\gamma{t}}$として打ち消されているので、OKと言えます。なお、時間が$ \dfrac{1}{\gamma} $経過すると、振幅$e^{\gamma{t}}$は$\dfrac{1}{e}$に縮小されていくので、この時間$T_d=\dfrac{1}{\gamma}$を減衰時間と言ったりもします。
過減衰 ($\gamma>\omega_0$ の場合)
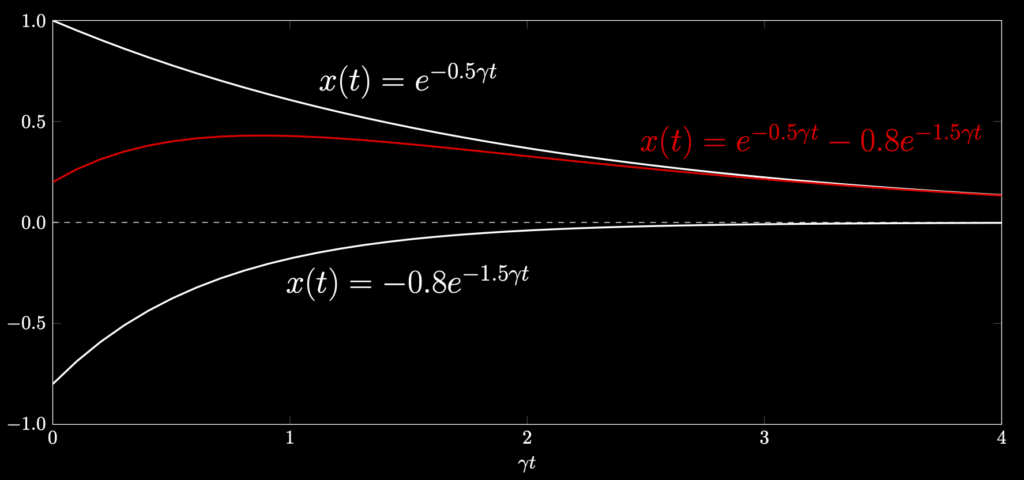
抵抗が強い場合、これは２つの急速に減衰していく$e$のマイナス乗の解を組み合せたものが解になるのでした。具体的には、２つの解 $e^{\alpha{t}}$:$$\alpha=-\gamma\pm\sqrt{\gamma^2-{\omega_0}^2}<0$$の一次結合が一般解で、共通の$e^{-\gamma{t}}$を括って、$$x(t)=e^{-\gamma{t}}\{C_1e^{+\sqrt{\gamma^2-{\omega_0}^2}t}+C_2e^{-\sqrt{\gamma^2-{\omega_0}^2}t}\}$$となります。グラフは、２つの減衰する解を足して、例えばこんな感じです。
臨界減衰 ($\gamma=\omega_0$ の場合)
では、ちょうど抵抗と角振動数が釣り合ってる場合はどうなるのでしょうか。実は、今まで使っていた２つの$\alpha$がルートが消えることにより、１つに減ってしまいます。すなわち、臨界減衰においては、$$\alpha=-\gamma\pm\sqrt{\gamma^2-{\omega_0}^2}=-\textcolor{black}{\gamma}{t}$$となってます。このままだと、２階の微分方程式を解かないといけないのに、独立な解は１つしかありません。そこで、「定数変化法」というアプローチを行います。これは、定数だと考えていた部分を、時間の関数だと捉え直して、もう一度微分方程式に代入する手法です。つまり、$$x(t)=Ae^{\alpha{t}}\ \rightarrow\ x(t)=\textcolor{red}{A(t)}e^{\alpha{t}}$$という風に、当初の$e^{\alpha{t}}$という解の仮定では拾い損ねた$A(t)e^{\gamma{t}}$という形の解を探してみるという考え方です。イメージとしてはこんな感じ。
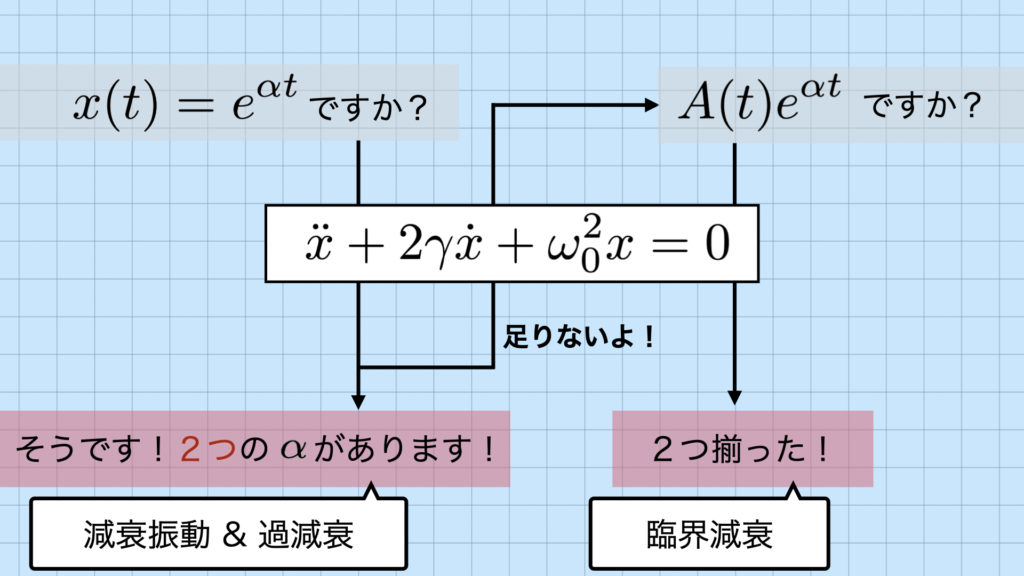
実際に$\dot{x}$と$\ddot{x}$を、積の微分法を使いながら計算して、微分方程式に入れると、めちゃくちゃ打ち消しが起こって、(後の例題のところで詳しく扱います。)$$\ddot{A}=0\ \ \therefore{A(t)=C_1t+C_2}$$が得られます。結局、臨界減衰の場合の一般解は、$$x(t)=e^{-\gamma{t}}(C_1t+C_2)$$となります。
一般解は、「減衰項$\times$(三角関数or指数関数or一次関数)」の形で書ける。
・減衰振動($\gamma<\omega_0$)
$$x(t)=e^{-\gamma{t}}\{C_1\cos(\omega_1{t})+C_2\sin(\omega_1{t})\}$$
・過減衰($\gamma>\omega_0$)
$$x(t)=e^{-\gamma{t}}\{C_1e^{+\sqrt{\gamma^2-{\omega_0}^2}t}+C_2e^{-\sqrt{\gamma^2-{\omega_0}^2}t}\}$$
・臨界減衰($\gamma=\omega_0$)
$$x(t)=e^{-\gamma{t}}(C_1t+C_2)$$
例題とその解説
例題を通して、全体をざっと復習します。問題はこちら。
運動方程式を立てて整理する
運動方程式を立てると、位置$x$の時間微分を$\dot{x}$として、$$m\ddot{x}=-kx-\lambda{\dot{x}}$$ここで、両辺を質量$m$で割って左辺に項を集めると、$$\ddot{x}+\frac{\lambda}{m}\dot{x}+\frac{k}{m}x=0$$となる。これは抵抗がない場合($\lambda=0$)に単振動の方程式になり、その角振動数を$\omega_0=\sqrt{k/m}$と置くと、$$\ddot{x}+\frac{\lambda}{m}\dot{x}+{\omega_0}^2x=0$$となる。このとき、$\dfrac{\lambda}{m}=2\gamma$とすれば、先ほどまで本文で扱っていた運動方程式と同じ形になる。
解を求める
次にこの微分方程式の解を求めます。最初に解いたときは、代入した後の計算が楽になるように、$x(t)=e^{\alpha{t}}$と仮定して解き始めました。微分方程式へ代入して得られる代数方程式は、$$\alpha^2+\frac{\lambda}{m}\alpha+\omega_0^2=0$$であり、解くと$$\alpha=-\frac{\lambda}{2m}\pm\sqrt{\bigg(\frac{\lambda}{2m}\bigg)^2-\omega_0^2}$$となります。先程までの話を思い返せば、ルートの中がプラスになる場合(抵抗$\lambda$が強いので「過減衰」)、マイナスになる場合(「減衰振動」)、ゼロになる場合(「臨界減衰」)の３つで変わりますが、どの場合においても減衰項は$e^{-\gamma{t}}=e^{-(\lambda/2m)t}$で、共通するのでした。異なるのは、それに掛かる部分で指数関数になるか、三角関数になるか、一次関数になるかという点でした。従って、解の仮定としていきなり$$x(t)=e^{-(\lambda/2m)t}\times{}A(t)$$として考えれば、あとはこの$A(t)$が満たす解を調べて確定させれば終わりになります。以降、$\gamma=\lambda/2m$として計算を進めます。(タイピングも大変だし、実際に計算する時もこのほうが楽です。) 一度$x$を微分すると、$$\dot{x}=(-\gamma{A}+\dot{A})e^{-\gamma{t}}$$もう一度微分すると、$$\ddot{x}=(\gamma^2A-2\gamma\dot{A}+\ddot{A})e^{-\gamma{t}}$$これらを微分方程式$$\ddot{x}+2\gamma{\dot{x}}+\omega_0^2{x}=0$$に代入します。全ての項に$e^{-\gamma{t}}$がくっついているので、先に割っておけば、$$(\gamma^2A-2\gamma\dot{A}+\ddot{A})+2\gamma(-\gamma{A}+\dot{A})+\omega_0^2A=0$$となるので、整理して、$$\ddot{A}+(\omega_0^2-\gamma^2)A=0$$ $A$に関する微分方程式となります。ここで、$\gamma=\omega_0$(臨界減衰)の時は、$$\ddot{A}=0\ \therefore{A(t)=C_1t+C_2}$$であり、$\omega_0>\gamma$(減衰振動)の時は、$$\ddot{A}=-(\omega_0^2-\gamma^2)A$$であり、これは角振動数を$\omega_1=\sqrt{\omega_0^2-\gamma^2}$とした単振動の方程式ですね。この振動の周期は、$$T=\frac{2\pi}{\omega_1}=\frac{2\pi}{\sqrt{\omega_0^2-\gamma^2}}>\frac{2\pi}{\omega_0}$$で、周期は単振動よりも伸びています。さらに、$\gamma>\omega_0$(過減衰)の時は、$$\ddot{A}=(\gamma^2-\omega_0^2)A$$であり、これは、２回微分すると正の数$\sqrt{\gamma^2-\omega_0^2}$が２つ、または負の数$-\sqrt{\gamma^2-\omega_0^2}$が２つ飛び出してくる微分方程式と読めるので、指数関数の方程式になっています。まとめます。
運動方程式:$$m\ddot{x}=-kx-\lambda{\dot{x}}\Leftrightarrow\ddot{x}+\frac{\lambda}{m}\dot{x}+{\omega_0}^2x=0$$より、解の形を$$x(t)=e^{-(\lambda/2m)t}\times{}A(t)$$と予想して代入すれば、$A(t)$の微分方程式: $$\ddot{A}=-(\omega_0^2-\gamma^2)A$$となり、$\gamma=\omega_0$(臨界減衰)の時は、$$\ddot{A}=0\ \therefore{A(t)=C_1t+C_2}$$で一次関数に、$\omega_0>\gamma$(減衰振動)の時は、角振動数を$\omega_1=\sqrt{\omega_0^2-\gamma^2}$とした単振動の三角関数となる。なお、振動の周期は、$$T=\frac{2\pi}{\omega_1}=\frac{2\pi}{\sqrt{\omega_0^2-\gamma^2}}>\frac{2\pi}{\omega_0}$$で、周期は単振動よりも伸びる。また、$\gamma>\omega_0$(過減衰)の時は、$$\ddot{A}=(\gamma^2-\omega_0^2)A$$であり、指数関数になる。
各節のまとめの再掲
それぞれの節でまとめた内容を再掲します。
バネ(自然長: $x=0$)に繋がれて振動している物体に、速度$\dot{x}$に比例した粘性抵抗が働いているときの運動方程式は、
$$m\ddot{x}=-kx-\lambda\dot{x}$$
であり、抵抗成分が微小であれば「減衰振動・不足減衰」、抵抗成分が強ければ「過減衰」、これらの境界が「臨界減衰」となる。
運動方程式 $m\ddot{x}=-kx-\lambda{\dot{x}}$ の両辺に速度 $v=\dot{x}$ を内積すると、$$mv\frac{dv}{dt}=-kx\frac{dx}{dt}-\lambda({\dot{x}})^2\ \ \cdots(A)$$となり、加速度由来の項は運動エネルギーの時間変化、復元力由来の項は弾性エネルギーの時間変化へ書き換えられるので、結局、運動方程式から$$\frac{d}{dt}\bigg(\frac{1}{2}mv^2+\frac{1}{2}kx^2\bigg)=-\lambda(\dot{x})^2$$が導ける。この式を見れば、力学的エネルギーが抵抗力の仕事により散失していくことがわかる。
運動方程式$ m\ddot{x}=-kx-\lambda{\dot{x}} $において、抵抗成分を$\lambda=2m\gamma$、(抵抗がない場合の)角振動数を$\omega_0=\sqrt{k/m}$とおくと、$$\ddot{x}+2\gamma\dot{x}+{\omega_0}^2x=0$$のようにまとめられる。ここで、解を$$x(t)=e^{\alpha{t}}$$と仮定して代入すれば、$e^{\alpha{t}}\neq0$として、$$\alpha^2+2\gamma\alpha+\omega_0^2=0$$より、$$\alpha=-\gamma\pm\sqrt{\gamma^2-{\omega_0}^2}$$ここで、$\gamma>\omega_0$の場合(過減衰)には、$\alpha$が負の実数となるために、急速に減衰していく振動しない解が得られ、一方、$\gamma<\omega_0$の場合(減衰振動)には、$\alpha$が複素数$-\gamma\pm{i}\omega_1$になるため、振動する解が得られる。
一般解は、「減衰項$\times$(三角関数or指数関数or一次関数)」の形で書ける。
・減衰振動($\gamma<\omega_0$)
$$x(t)=e^{-\gamma{t}}\{C_1\cos(\omega_1{t})+C_2\sin(\omega_1{t})\}$$
・過減衰($\gamma>\omega_0$)
$$x(t)=e^{-\gamma{t}}\{C_1e^{+\sqrt{\gamma^2-{\omega_0}^2}t}+C_2e^{-\sqrt{\gamma^2-{\omega_0}^2}t}\}$$
・臨界減衰($\gamma=\omega_0$)
$$x(t)=e^{-\gamma{t}}(C_1t+C_2)$$
運動方程式:$$m\ddot{x}=-kx-\lambda{\dot{x}}\Leftrightarrow\ddot{x}+\frac{\lambda}{m}\dot{x}+{\omega_0}^2x=0$$より、解の形を$$x(t)=e^{-(\lambda/2m)t}\times{}A(t)$$と予想して代入すれば、$A(t)$の微分方程式: $$\ddot{A}=-(\omega_0^2-\gamma^2)A$$となり、$\gamma=\omega_0$(臨界減衰)の時は、$$\ddot{A}=0\ \therefore{A(t)=C_1t+C_2}$$で一次関数に、$\omega_0>\gamma$(減衰振動)の時は、角振動数を$\omega_1=\sqrt{\omega_0^2-\gamma^2}$とした単振動の三角関数となる。なお、振動の周期は、$$T=\frac{2\pi}{\omega_1}=\frac{2\pi}{\sqrt{\omega_0^2-\gamma^2}}>\frac{2\pi}{\omega_0}$$で、周期は単振動よりも伸びる。また、$\gamma>\omega_0$(過減衰)の時は、$$\ddot{A}=(\gamma^2-\omega_0^2)A$$であり、指数関数になる。
参考
・京都大学OCW「振動・波動論」https://ocw.kyoto-u.ac.jp/course/330/
