力学の全体像

詳しい内容を学習する前に全体像を把握することは進む方向を定める事ができる、 という意味で大変有効です。 そこで、 このページでは、 力学は何を学ぶ学問なのか？その目的は何なのか？という事に焦点を絞った話をしていこうと思います。

力学の目標

力学とは、 「自然界にどのような力があるのかは与えられたものとして、 その力による物体の運動を論じる学問」のことをいいます。(出典: 山本義隆『新・物理入門』)　その、 物体の運動(motion・物体の位置変化)を知るためには、 「いつ」「どこに」物体がわかれば良いわけです。　数学の言葉を使えば、 物体の位置の関数$x(t)$を求めることと言えます。(一次元の場合。)　関数の形が分かっていれば、 時刻$t$と位置$x$の対応がわかり、 物体の運動が理解できます。

力学の原理「運動方程式」

その位置の関数$x(t)$を求める根拠となるのが「運動方程式」です。 これは力学の原理であり、 すべてのスタート地点となる方程式です。

$$m\frac{dv}{dt}=F$$

この方程式は、 次のように解釈します。「注目することを決めた粒子(質量$m$)に対して、 力$F$が働いたならば、 その結果として加速度$\frac{dv}{dt}$が生じる」

運動方程式の”解釈”を元にして、 粒子の運動を追跡する方法を次のようにまとめてみます。

運動方程式と位置の関数の繋がり

ここまでで、 力学の目標は物体の位置の関数$x(t)$を求めることであり、 その根拠は運動方程式であること、 生じた加速度が求められることを確認しました。

次に行うことは、 手に入れた加速度から何とかして目的の関数$x(t)$を求めることです。

さて、 物体の速度(velocity)が「微小時間$dt$における位置の変化量」であることは既知の事実であると思います。 数学を使うと速度は次のように書く事ができます。

$$v(t)=\frac{x(t+dt)-x(t)}{dt}\ (=\frac{dx}{dt})$$

これが物体の速度の定義であり、 位置の変化$x(t+dt)-x(t)$を微小時間$dt$で割って求める事ができます。 実際の計算では、 与えられた位置の関数$x(t)$を時間で微分して求めます。

位置の関数を時間微分して速度の関数$v(t)$を得たのなら、 その速度の関数も時間微分してみたくなってしまいます。

$$a(t)=\frac{v(t+dt)-v(t)}{dt}\ (=\frac{dv}{dt}=\frac{d^2x}{dt^2})$$

このように定義される量のことを加速度(acceleration)と言い、 微小時間における速度の変化量です。

加速度と位置の関数は２回の時間微分によって関係付けられている事がわかりました。　ここまでの内容をすべてまとめます。

加速度から位置変化を求める

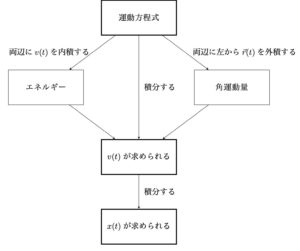
運良く積分が実行できるのなら、 定義を逆に登るように、 次の式から任意の時間における粒子の速度$v(t)$が求められ、 さらに$x(t)$が求められます。

$$v(t)=v(0)+\int_0^{t}a(t)dt$$

$$x(t)=x(0)+\int_0^{t}v(t)dt$$

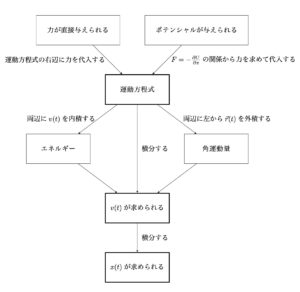
ただし、 すべての場合でこの式が利用できるわけではありません。 しかしそんな時は諦めるのではなく、 「エネルギー」や「角運動量」という量に注目して何とか積分を実行します。(詳しくは別のページで。)

運動方程式を立式したあとの流れをまとめた図を載せておきます。

力はどうか

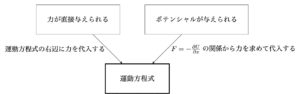
ここまでは、 運動方程式を立式したあとの話を述べてきましたが、 力についても確認しておきます。 力の与えられ方は大きく分けて２つです。 １つは問題設定で示されている場合。 もう１つはポテンシャル(エネルギー)$U(x)$として与えられる場合です。

前者についてはそのまま運動方程式に代入、 後者については位置で微分したものにマイナスを付ければ力になる$F=-\frac{dU}{dx}$という関係を利用して力を求めます。 こちらも次の図の通りです。

総まとめ

すべてをまとめます。

今後は、 与えられた力の種類によって、 位置や速度がどのように振舞うのかを考えていくことになります。