微小な変化量を足し上げる

今回は、もっとも簡単な１次元での積分の例
$$x(t_2)-x(t_1)=\int_{t_1}^{t_2}v{\ dt}$$
を題材に、“足し上げる” 感覚を理解することを目標にします。

微小な変化量とは

位置$\ x\ $が時刻$\ t\ $から時刻$\ t+dt\ $($dt$は微小な時間)にかけて変化した状況を考えます。その変化分は、引き算の形で、
$$x(t+dt)-x(t)=dx$$
の左辺のように表し、右辺のように１つの記号で書くこともできます。ここで大切なのが、

$d$●を見たら、引き算であると捉えること

という捉え方です。この引き算は次のように考えるとイメージがしやすいです:

$$x(未来)-x(過去)$$

要するに、先の時刻の位置$x$から昔の時刻の位置$x$を引く操作です。過去の時刻を基準に、未来の時刻での位置を見ている、と捉えても良いでしょう。

引き算であることのありがたさ

次に、考える時間を少し長くして、時刻$\ t,t+dt,t+2dt\ $にて、位置が変化していくとします。図にするなら、このような状況。

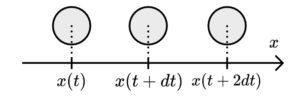
この場合の位置変化をそれぞれ、微小時間$\ dt\ $ごとに書き出すと、

$x(t+dt)-x(t)$

$x(t+2dt)-x(t+dt)$

ですが、この２式を足し合わせると、
$$x(t+2dt)-x(t)$$
となります。この計算で注目すべきなのは、

途中の時刻$\ t+dt\ $での値$\ x(t+dt)\ $が消えている

ことです。

もっと長い時間で考える

さらに長い時間で考えてみましょう。今度は、時刻$\ t_1,\ $ $t_1+dt,\ $ $t_1+2dt,\ \cdots,\ $ $t_2-dt,\ $ $t_2\ $(すなわち時刻$t_1$〜時刻$t_2$)にて位置が変化していくとします。この場合の位置変化を、先程と同様に、微小時間$\ dt\ $ごとに書き出すと、

$x(t_1+dt)-x(t_1)$

$x(t_1+2dt)-x(t_1+dt)$

$\vdots$

$x(t_2)-x(t_2-dt)$

となり、この式を全て足し上げると
$$x(t_2)-x(t_1)$$
となります。この場合も同様に、途中の時刻の値が全て消えていて、

最初の値$\ x(t_1)\ $と最後の値$\ x(t_2)\ $のみが残っている

ことに注目です。

速度$\ v\ $との関係

実際の問題を解く際には、速度$\ v(t)\ $が与えられて、そこから位置変化を求めてくださいと問われることが多いです。

さて、速度の定義は、

$$v(t)=\frac{dx}{dt}$$

ですが、ここで、右辺の分子に今まで扱っていた$\ dx\ $が登場しています。これを取り出すために両辺に$\ dt\ $をかけて両辺を交換すると、

$$dx=v(t)\ dt$$

となります。上での経験から、$d$●を見たら途中の$dt$ごとに書き出して足し上げて見たくなります。時刻$t_1$〜時刻$t_2$で考えると、左辺は

$$x(t_2)-x(t_1)$$

となり、一方の右辺$\ v(t)\ dt\ $は、

時刻により値が変わる$v(t)$が掛かっている

という違いがあります。つまり、途中の時刻の値がキャンセルされず、左辺のような全体での綺麗な打ち消しは起こらないわけです。よって、右辺ではそのようなラッキーは諦めて、単にシグマ記号で

$$\sum_{t=t_1}^{t_2}{v(t)dt}$$

と書きます。ここで、$\ dt\ $は、$\Delta{t}→0$の意味ですから、この右辺は極限の記号を用いて、

$$\lim_{\Delta{t}→0}{\ \sum_{t=t_1}^{t_2}{v(t)\Delta{t}}}$$

とも書くことができます。これは数学では区分求積法と呼ばれ、簡潔に

$$\int_{t_1}^{t_2}{v(t)dt}$$

と表すことができます。以上より、

$$x(t_2)-x(t_1)=\int_{t_1}^{t_2}{v(t)dt}$$

の関係が得られました。

今回の要点