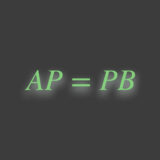数ベクトル空間 $\mathbb{R}^n$ から $\mathbb{R}^m$ への線形写像では、どんな形でも行列を左から掛けることで表すことができました。では、一般のベクトル空間の間の線形写像はどうでしょうか。実はこの場合も行列を用いて理解することができます。そのような行列を「表現行列」と呼びます。
目次
線形写像を調べる「基底を送って様子見」
線形写像 $\varphi{:}$ $V→W$ を考えてみます。ベクトル空間 $V$ の基底を
$$\mathcal{A}=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})$$
ベクトル空間 $W$ の基底を、
$$\mathcal{B}=(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})$$
とします。基底は大切な元なので、赤色にしておきます。(なお、今後 $V$ や $W$ にもう1つ基底を導入する際には、区別するために青色にします。)ここで、$\mathrm{dim}V=n,$ $\mathrm{dim}W=m$ となっていて、$V$と$W$の次元が違う場合があることに注意してください。
さて、今回の目標は、線形写像を行列で表してみることです。まずはこの線形写像の様子を調べるために、定義域 $V$ の基底を1つ送ってみましょう。
上の線形写像の、特に、$m=n$(定義域と終域の次元が一致している)の場合、
$${\textcolor{red}{\vec{w_i}}}=\varphi(\textcolor{red}{\vec{v_i}})\ (i=1,\ldots, n)$$
を満たすものがただ1つだけ存在します。これはすなわち、線形写像の基底の行き先を指定することで、全ての元の行き先が指定できるといえます。例えば、適当な $V$ の元を持ってきて、これが $\vec{v}$ $=$ $5\textcolor{red}{\vec{v_2}}+$ $3\textcolor{red}{\vec{v_4}}$ と書けたとします。ここで、基底の行き先が $\varphi(\textcolor{red}{\vec{v_2}})=\textcolor{red}{\vec{w_2}},$ $\varphi(\textcolor{red}{\vec{v_4}})=\textcolor{red}{\vec{w_4}}$ と指定されていた場合、$\varphi$ は線形写像なので、$\varphi(\vec{v})=5\textcolor{red}{\vec{w_2}}+3\textcolor{red}{\vec{w_4}}$ とわかります。
結局、基底の行き先を知っていれば十分といえます。
送られた元は、行き先のベクトル空間 $W$ の基底 $\mathcal{B}$ の一次結合で表せるので、基底 $\mathcal{B}$ に関する座標 $[\ ]_{\mathcal{B}}$ を用いて次のようになります。
$$\varphi(\textcolor{red}{\vec{v_1}})=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ [\varphi(\textcolor{red}{\vec{v_1}})]_{\mathcal{B}}$$
同じ調子で、残りの基底も送ってみましょう。
$$\varphi(\textcolor{red}{\vec{v_2}})=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ [\varphi(\textcolor{red}{\vec{v_2}})]_{\mathcal{B}}\\ \vdots\\ \varphi(\textcolor{red}{\vec{v_n}})=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ [\varphi(\textcolor{red}{\vec{v_n}})]_{\mathcal{B}}$$
基底変換行列のときと様子が似ています。
$$\textcolor{blue}{\vec{v_i}^{\prime}}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ [\textcolor{blue}{\vec{v_i}^{\prime}}]_{\mathcal{A}}\ (i=1,\ldots, n)$$
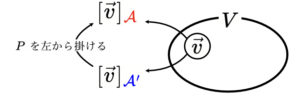
これを$1$から$n$まで順に並べると、左辺には基底 $\mathcal{A}^{\prime}$ が、右辺には基底 $\mathcal{A}$ と、成分が座標の行列(基底変換行列) $P$ が出てきました:
$$\underbrace{(\textcolor{blue}{\vec{v_1}^{\prime}},\textcolor{blue}{\vec{v_2}^{\prime}},\ldots,\textcolor{blue}{\vec{v_n}^{\prime}})}_{\mathcal{A}^{\prime}}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ P$$
また、任意の元 $\vec{v}\ (\in{V})$ について、「基底$\mathcal{A}^{\prime}$を使って書き、それを$P$で基底を$\mathcal{A}$へ変換したもの」と、「基底$\mathcal{A}$を使って書いたもの」を比較することで、任意の元 $\vec{v}$ についての座標の関係が得られました。
$$P\ [\vec{v}]_{\textcolor{blue}{\mathcal{A}^{\prime}}}=[\vec{v}]_{\textcolor{red}{\mathcal{A}}}$$
図で表すとこんな感じ。
詳しい説明は↓のページにあります。
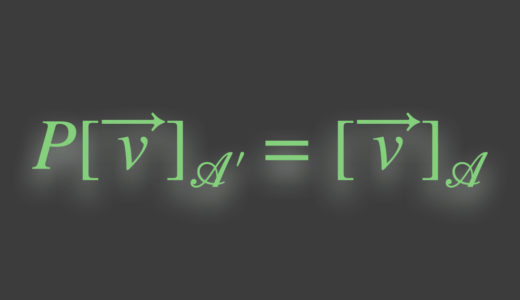 基底と座標と基底変換行列【例題付き】
基底と座標と基底変換行列【例題付き】
これらを並べます。座標を横に並べた成分から構成される行列を
$$A=\bigg[{[\varphi(\textcolor{red}{\vec{v_1}})]_{\mathcal{B}},[\varphi(\textcolor{red}{\vec{v_2}})]_{\mathcal{B}},\ldots,[\varphi(\textcolor{red}{\vec{v_n}})]_{\mathcal{B}}}\bigg]$$
とおけば、
$$(\varphi(\textcolor{red}{\vec{v_1}}),\varphi(\textcolor{red}{\vec{v_2}}),\ldots,\varphi(\textcolor{red}{\vec{v_n}}))\\\ \\=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ A\cdots(*)$$
となり、$V$ の基底を送ったものと $W$ の基底の関係が得られました。ここで、この式は基底変換行列 $P$ に関する式と同じ構造ですが、左辺の元たちは別に基底とは限らないことに注意してください。今は送り先のベクトル空間 $W$ の上での話であり、そこの基底の数は $m$ と約束したので、左辺の $n$ 個 では基底の数が合わないからです。
座標の対応「任意の元に関する対応関係」
次に、任意の元に関する座標の対応を見てみましょう。基底変換行列のときと同じ流れをとるなら、結局、元 $\vec{v}$ を送ったものが、
$$\varphi(\vec{v})=(\varphi(\textcolor{red}{\vec{v_1}}),\varphi(\textcolor{red}{\vec{v_2}}),\ldots,\varphi(\textcolor{red}{\vec{v_n}}))\ [?]_{?}$$
のように書ければ同様の手続きをなぞる事ができます。ただ、$\varphi(\vec{v_i})$ は $W$ の基底ではないため、「?」に何が入るかは詳しく調べないとわかりません。 $V$ の元は、基底 $\mathcal{A}$ を使って次のように書けました。
$$\vec{v}=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})\ [\vec{v}]_{\mathcal{A}}\\\ \\=c_1\textcolor{red}{\vec{v_1}}+\ldots+c_n\textcolor{red}{\vec{v_n}}$$
この元を $\varphi$ で送ると、
$$\varphi(\vec{v})=\varphi(c_1\textcolor{red}{\vec{v_1}}+\ldots+c_n\textcolor{red}{\vec{v_n}})\\ \ \\=c_1\varphi(\textcolor{red}{\vec{v_1}})+\ldots+c_n\varphi(\textcolor{red}{\vec{v_n}})\\\ \\=(\varphi(\textcolor{red}{\vec{v_1}}),\varphi(\textcolor{red}{\vec{v_2}}),\ldots,\varphi(\textcolor{red}{\vec{v_n}}))\ [\vec{v}]_{\mathcal{A}}$$
となります。2行目への変形は、$\varphi$ が線形写像なので、実数倍と足し算がバラせることを利用しました。では早速$(*)$式を使います。
$$\varphi(\vec{v})=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ A\ [\vec{v}]_{\mathcal{A}}$$
ところで、$\varphi(\vec{v})$ を $W$ の基底 $\mathcal{B}$ を使うと、
$$\varphi(\vec{v})=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ [\varphi(\vec{v})]_{\mathcal{B}}$$
と書けます。元は、同一の基底を用いると一次結合でただ一通りに表せるので、
$$A\ [\vec{v}]_{\mathcal{A}}=[\varphi(\vec{v})]_{\mathcal{B}}$$
という座標の関係が得られます。この関係を図示すると次のようになります。
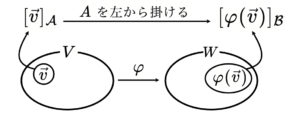
このような行列 $A$ を基底 $\mathcal{A},\mathcal{B}$ に関する $\varphi$ の表現行列といいます。以上の内容をまとめます。
$$A=\bigg[{[\varphi(\textcolor{red}{\vec{v_1}})]_{\mathcal{B}},[\varphi(\textcolor{red}{\vec{v_2}})]_{\mathcal{B}},\ldots,[\varphi(\textcolor{red}{\vec{v_n}})]_{\mathcal{B}}}\bigg]$$
であり、
$$(\varphi(\textcolor{red}{\vec{v_1}}),\varphi(\textcolor{red}{\vec{v_2}}),\ldots,\varphi(\textcolor{red}{\vec{v_n}}))\\\ \\=\underbrace{(\textcolor{red}{\vec{w_1}},\textcolor{red}{\vec{w_2}},\ldots,\textcolor{red}{\vec{w_m}})}_{\mathcal{B}}\ A$$
となり、座標の間には次の関係が成り立つ。
$$A\ [\vec{v}]_{\mathcal{A}}=[\varphi(\vec{v})]_{\mathcal{B}}$$
表現行列についての例題
$$\vec{a}_1= \left(\begin{array}{c} 2\\ 0\\ 1 \end{array} \right), \vec{a}_2= \left(\begin{array}{c} 1\\ 1\\ 0 \end{array} \right), \vec{a}_3= \left(\begin{array}{c}0\\ -1\\ 1 \end{array}\right)\\ \ \\\vec{b}_1= \left(\begin{array}{c} 1\\ -1\\ 2 \end{array} \right), \vec{b}_2= \left(\begin{array}{c} 2\\ 2\\ -1 \end{array} \right), \vec{b}_3= \left(\begin{array}{c}0\\ 1\\ -1 \end{array}\right)$$
として、$\mathbb{R}^3$の基底 $\mathcal{A}=(\vec{a}_1,\vec{a}_2,\vec{a}_3)$ と $\mathcal{B}=(\vec{b}_1,\vec{b}_2,\vec{b}_3)$ を考える。線形写像$\varphi:\mathbb{R}^3→\mathbb{R}^3$ を
$$\varphi(\vec{a}_1)= \left(\begin{array}{c} 3\\ 3\\ -1 \end{array} \right), \varphi(\vec{a}_2)= \left(\begin{array}{c} 1\\ -3\\ 4 \end{array} \right), \varphi(\vec{a}_3)= \left(\begin{array}{c} 0\\ 1\\ -1 \end{array} \right)$$で定義する。このとき、基底$\mathcal{A}$に関する$\varphi$の表現行列$A$と、基底$\mathcal{B}$に関する$\varphi$の表現行列$B$を求めよ。
問題を解くまえに、「座標の関係から元の関係を導く」と「表現行列そのものから元の関係を導く」で、表現行列に関する元の関係の式の導き方を二通りで確認します。その後、「表現行列$A$を求める」で $A$ を実際に求めます。こちらは問題で与えられている条件が行いたい計算にあっているのですぐに求めることができます。一方 $B$ は「表現行列$B$を求める(素直に)」と「表現行列$B$を求める(基底の変換による表現行列の変化)」の二通りで考えていますが、前者は素直なやり方、後者は $A$ と $B$ の関係が基底変換行列 $P$ で書けることを利用したやり方です。
座標の関係から元の関係を導く
まずは、表現行列 $A$ について考えます。
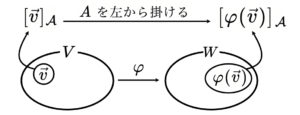
一番覚えやすく、間違えにくいのは座標の関係だと思います。
$$A[\vec{v}]_{\mathcal{A}}=[\varphi(\vec{v})]_{\mathcal{A}}$$
ここでは、この座標の関係式から、元(げん)の関係を導いてみます。座標について思い出すと、
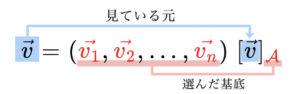
という構造なので、座標から元を復元するためには、選んだ基底を左側に添えればいいわけです。すなわち、
$$(\vec{a}_1, \vec{a}_2, \vec{a}_3)\ A[\vec{v}]_{\mathcal{A}}=(\vec{a}_1, \vec{a}_2, \vec{a}_3)\ [\varphi(\vec{v})]_{\mathcal{A}}$$
この右辺は $\varphi(\vec{v})$ そのものを表しているので、結局、
$$(\vec{a}_1, \vec{a}_2, \vec{a}_3)\ A[\vec{v}]_{\mathcal{A}}=\varphi(\vec{v})\cdots\ ①$$
となります。ところで、$\varphi(\vec{v})$ は
$$\varphi(\vec{v})=(\varphi(\vec{a}_1),\varphi(\vec{a}_2),\varphi(\vec{a}_3))[\vec{v}]_{\mathcal{A}}\cdots\ ②$$
と書けるので(詳しくはここら辺)、①式と②式から
$$(\varphi(\vec{a}_1),\varphi(\vec{a}_2),\varphi(\vec{a}_3))=(\vec{a}_1, \vec{a}_2, \vec{a}_3)\ A\cdots\ (*)$$
という元の関係を得られました。
表現行列そのものから元の関係を導く
表現行列は座標を横に並べた成分から構成される行列でした。$A$をダイレクトに書き下すと、
$$A=\bigg[{[\varphi(\vec{a}_1)]_{\mathcal{A}},[\varphi(\vec{a}_2)]_{\mathcal{A}},[\varphi(\vec{a}_3)]_{\mathcal{A}}}\bigg]$$
であり、言葉でいうなら「定義域の基底を送り、それを送り先の基底で眺めた座標を並べたもの」といった感じでしょうか。これを覚えているなら、$A$ の各成分は座標なので、基底$\mathcal{A}$を左に並べれば、眺めていた元を取り出せて、
$$(\varphi(\vec{a}_1),\varphi(\vec{a}_2),\varphi(\vec{a}_3))=(\vec{a}_1, \vec{a}_2, \vec{a}_3)\ A\cdots\ (*)$$
という元の関係が同様に得られます。
表現行列$A$を求める
では実際に $A$ を求めてみましょう。今は、元の関係$(*)$式の左辺 $\varphi(\vec{a}_1),$ $\varphi(\vec{a}_2),$ $\varphi(\vec{a}_3)$ が問題によって全て指定されています。したがって即座に
$$\underbrace{\left[ \begin{array}{ccc} 3&1&0\\ 3&-3&1\\ -1&4&-1 \end{array} \right]}_{B_1}=\underbrace{\left[\begin{array}{ccc} 2&1&0\\ 0&1&-1\\ 1&0&1 \end{array}\right]}_{A_1}A$$
を解けばいいとわかります。$A_1$の逆行列$A_1^{-1}$を求めて、$B_1$に左から掛ければ$A$を求められますが、$A_1^{-1}$を求めるための「$A_1$から単位行列を作る行基本変形」を$B_1$にも同時に施せば一発で$A_1^{-1}B_1$を求めることができます。(基底変換行列の例題「ダイレクトに求める」) すなわち、$[A_1|B_1]$を簡約化します。
$$\left[\begin{array}{ccc|ccc} 2&1&0&3&1&0\\ 0&1&-1&3&-3&1\\ 1&0&1&-1&4&-1\end{array}\right]→\cdots\\\ \\→\left[\begin{array}{ccc|ccc}1&0&0&1&0&0\\0&1&0&1&1&0\\0&0&1&-2&4&-1\end{array}\right]$$
表現行列$B$を求める(素直に)
今度は $B$ を求めます。$B$に関する元の関係は、
$$(\varphi(\vec{b}_1),\varphi(\vec{b}_2),\varphi(\vec{b}_3))=(\vec{b}_1, \vec{b}_2, \vec{b}_3)\ B$$
です。ただ、この左辺は問題で具体的に与えられていないため、自分で求める必要があります。わかっていることは、基底 $\mathcal{A}$ の行き先だけなので、基底$\mathcal{B}$ を $\mathcal{A}$ を使って書けば、線形写像の性質から $\mathcal{B}$ の行き先も判明します。ここで役立つのが基底変換行列です。基底 $\mathcal{A}$ から $\mathcal{B}$ への基底変換行列を $P$ としたとき、
$$(\vec{b}_1, \vec{b}_2, \vec{b}_3)=(\vec{a}_1, \vec{a}_2, \vec{a}_3)P$$
という基底の関係式が成り立ちます。$P$ は座標から構成されている
$$P=\bigg[{[\vec{b_1}]_{\mathcal{A}},[\vec{b_2}]_{\mathcal{A}},[\vec{b_3}]_{\mathcal{A}}}\bigg]$$
ため、1つ1つの基底についても関係がわかります。
実は、この例題は「基底変換行列についての例題」で扱ったものと同じで、そちらで基底変換行列 $P$ は求めていました。
$$P=\left[ \begin{array}{ccc} 0&1&0\\ 1&0&0\\ 2&-2&-1 \end{array} \right]$$
だったので、基底 $\mathcal{B}$ は次のようにそれぞれ表せます。
$$\vec{b}_1=(\vec{a}_1, \vec{a}_2, \vec{a}_3)[\vec{b}_1]_{\mathcal{A}}=\vec{a}_2+2\vec{a}_3\\\ \\\vec{b}_2=(\vec{a}_1, \vec{a}_2, \vec{a}_3)[\vec{b}_2]_{\mathcal{A}}=\vec{a}_1-2\vec{a}_3\\\ \\\vec{b}_3=(\vec{a}_1, \vec{a}_2, \vec{a}_3)[\vec{b}_3]_{\mathcal{A}}=-\vec{a}_3$$
したがって、
$$\varphi(\vec{b}_1)=\varphi(\vec{a}_2)+2\varphi(\vec{a}_3)=\left( \begin{array}{c} 1\\ -1\\ 2 \end{array} \right)\\\ \\\varphi(\vec{b}_2)=\varphi(\vec{a}_1)-2\varphi(\vec{a}_3)=\left( \begin{array}{c} 3\\ 1\\ 1 \end{array} \right)\\\ \\\varphi(\vec{b}_3)=-\varphi(\vec{a}_3)=\left( \begin{array}{c} 0\\ -1\\ 1 \end{array} \right)$$
となります。これ以降は表現行列 $A$ の場合と同じ手順です。表現行列 $B$ に関する元の関係から、
$$\underbrace{\left[ \begin{array}{ccc} 1&3&0\\ -1&1&-1\\ 2&1&1 \end{array} \right]}_{B_2}=\underbrace{\left[\begin{array}{ccc} 1&2&0\\ -1&2&1\\ 2&-1&-1 \end{array}\right]}_{A_2}B$$
であり、あとは $[A_2|B_2]$ を簡約化して終わりです。
$$\left[\begin{array}{ccc|ccc} 1&2&0&1&3&0\\ -1&2&1&-1&1&-1\\ 2&-1&-1&2&1&1\end{array}\right]→\cdots\\\ \\→\left[\begin{array}{ccc|ccc}1&0&0&1&1&0\\0&1&0&0&1&0\\0&0&1&0&0&-1\end{array}\right]\\\ \\\therefore{B}=\left[\begin{array}{ccc}1&1&0\\0&1&0\\0&0&-1\end{array}\right]$$
表現行列$B$を求める(基底の変換による表現行列の変化)
上では素直に $\varphi(\vec{b}_i)$ を求めてから $B$ を考えましたが、次の話も知っておくと便利です。
- 基底$\mathcal{A}$に関する表現行列を$A$
- 基底$\mathcal{B}$に関する表現行列を$B$
- 基底$\mathcal{A}$から$\mathcal{B}$への基底変換行列を$P$
とする。このとき、次式が成り立つ。
$$AP=PB$$
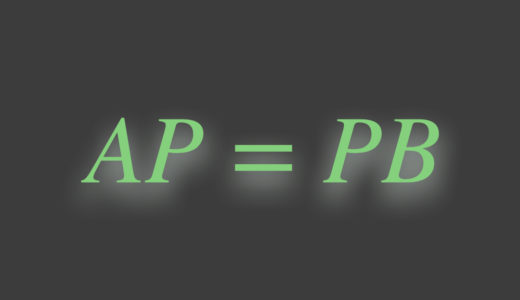 表現行列の変化
表現行列の変化
「基底 $\mathcal{A}$ に関する表現行列 $A$ 」と「基底 $\mathcal{A}$ から $\mathcal{B}$ への基底変換行列 $P$ 」を知っている場合、新たに導入した基底 $\mathcal{B}$ に関する表現行列 $B$ は、
$$B=P^{-1}AP$$
で求めることができます。まずは $AP$ を先に計算しておくと、
$$AP=\left[\begin{array}{ccc}1&0&0\\1&1&0\\-2&4&-1 \end{array}\right] \left[\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 2&-2&-1 \end{array}\right]\\\ \\= \left[\begin{array}{ccc}0&1&0\\1&1&0\\2&0&1 \end{array}\right]$$
であり、$B$ は、
$$B=P^{-1} \underbrace{\left[\begin{array}{ccc} 0&1&0\\ 1&1&0\\ 2&0&1 \end{array}\right]}_{AP}$$
から得られます。$P$ の逆行列を求める基本変形 を$AP$ にも同時に施せば直接計算できます。すなわち $[P|AP]$ の簡約化をします。
$$\left[\begin{array}{ccc|ccc} 0&1&0&0&1&0\\ 1&0&0&1&1&0\\ 2&-2&-1&2&0&1\end{array}\right]→\cdots\\\ \\→\left[\begin{array}{ccc|ccc}1&0&0&1&1&0\\0&1&0&0&1&0\\0&0&1&0&0&-1\end{array}\right]\\\ \\\therefore{B}=\left[\begin{array}{ccc}1&1&0\\0&1&0\\0&0&-1\end{array}\right]$$
素直に求める場合と比べて、こちらのほうが計算量は少ないように感じました。
表現行列の変化へ続く… ↓
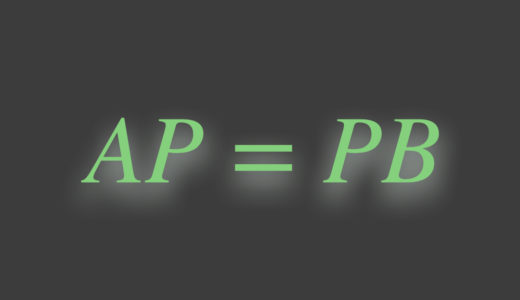 表現行列の変化
表現行列の変化