慣性抵抗の問題を解いてみる

　「例題→解説」の形式で、速度の２乗に比例する抵抗力「慣性抵抗」が働く粒子の運動を考えます。計算が重めですが、計算を素早く進めるコツや、覚えるときに注目するといい部分も書いてあります。

　記事の構成としては、まず運動方程式の立て方について。次に、一般解を求める前に読み取れる「終端速度」について見てみます。そして、解を双曲線関数として仮定してから解く方法と、変数分離形で解く方法の２パターンを扱います。ぜひ、この記事を参考に自分の手で計算を行って、「慣性抵抗」をマスターしてください。

「粘性抵抗」や「減衰振動」の解き方は別の記事↓に書いてあります。

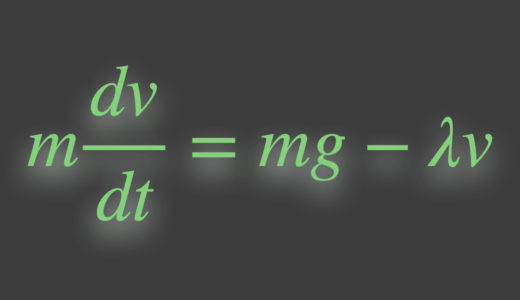2021年6月12日自由落下と粘性抵抗

2021年6月1日減衰振動【例題付き】

慣性抵抗の問題

　速度$v(t)$の２乗に比例する抵抗力(慣性抵抗)を受ける粒子の運動を考えてみましょう。この力は、粒子が流体に当たることによって生じる抵抗です。

　まず、この手の問題で大切なのは初期条件の把握です。最初の時刻($t=0$)で、「どの位置$x(0)$」にいて、「どんなスピード$v(0)$」かを確認することから問題を解き始めましょう。この条件をベースに、粒子は位置$x$と速度$v$を変化させていきます。今回は、$v(0)=0,$ $x(0)=0$が読み取れていればokです。

力を正確に把握して運動方程式を立てる

　次に考えるのは運動方程式です。粒子に作用している力を「漏れなく・正確に(符号間違えせずに)」探しましょう。今回は「重力$-mg$」と「慣性抵抗$+\kappa{v^2}$」です。

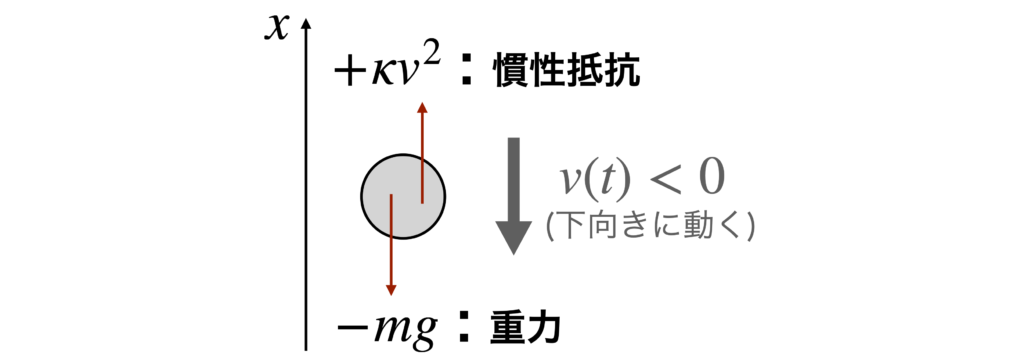
力の符号については、座標軸$x$を基準に考えます。今回は問題で示されているように、上向きがプラスの方向なので、それと逆に向いているという意味で重力にはマイナスが付きます。(逆に、下向きがプラスになるように座標軸が導入されていた場合、重力は$+mg$になります。)

　もう１つの慣性抵抗については、落下運動を考えているため、粒子は下向きに動きます。したがって、その動きに抵抗する向き(上向き)に力が働くので慣性抵抗にはプラスが付きます。

以上のようにして、粒子に作用する力を把握します。これらの力を右辺に書いた運動方程式は次のようになります。

$$m\frac{{d}{v}}{{d}{t}}=-mg+\kappa{v}^2$$

ちなみに、運動方程式の左辺にある「加速度」を表す$dv/dt$は、位置の２階微分で$d^2x/dt^2$とも書けますが、右辺に登場している変数$v$に合わせて$dv/dt$と書いています。他の問題で、右辺に変数$x$がでた場合(位置に比例した力をバネから受ける場合など)には、左辺の加速度は$d^2x/dt^2$とするといいでしょう。

微分方程式の一般解を求めなくても読み取れる情報

　この微分方程式を、先ほど確認した初期条件の下で解けば、任意の時刻$t$における粒子の速度$v(t)$を知ることができます。まず、最初の時刻$t=0$では、$v=0$なので、運動方程式は右辺の抵抗力が$0$になり、

$$m\frac{{d}{v}}{{d}{t}}=-mg+0\ <0$$

となります。$v(t)$の導関数である$dv/dt$が負の値をとっているため、速度$v(t)$は減少することがわかります。ところが、しばらく時間が経過することで速度が$0$ではなくなると、抵抗力が生じることで、速度の変化$dv/dt$は$0$へ近づきます。したがって、十分に時間が経過すれば($t→\infty$とすれば)、速度$v$は一定値に落ち着いてしまいます。このことを式で考えてみましょう。$t→\infty$で、$dv/dt=0,$ $v→v_{\infty}$となると考えて、運動方程式の左辺を$0$にして、右辺の速度を$v_{\infty}$にすると、

$$m\cdot{0}=-mg+\kappa{v_{\infty}}^2\ \ \therefore{v_{\infty}}=-\sqrt{\frac{mg}{\kappa}}$$

となります。この、最終的に落ち着く速度のことを「終端速度$v_{\infty}$」と呼びます。(今回は$v(t)<0$の状況を考えているため、係数はマイナスを選びます。)

　ここで、質量$m$はルートの中の分子に入っていることの意味を定性的に確認しておきましょう。質量が大きいと、重力の加速させる効果が慣性抵抗よりも大きいために、終端速度が大きくなります。なので、$m$が大きくなったら$v_{\infty}$も大きくなります。

実際に運動方程式を解いてみよう($\tanh$を使って)

(変数分離法はこの次の節で扱います。)

　運動方程式:

$$m\frac{{d}{v}}{{d}{t}}=-mg+\kappa{v}^2$$

を実際に解いてみましょう。これまでの単振動、粘性振動、粘性抵抗のある落下…などの運動方程式を解いた経験を総動員して解がないか探索してみます。例えば、複素数$\alpha$を使った$v=Ce^{-\alpha{t}}$という解は振動現象や過渡現象に対してかなり有効な解でした。しかし代入しても、２乗にする部分があるために求まりません。諦めずに、「定数変化法」でトライしてみましょう。これは、これまで定数だと思っていた$C$を時間の関数$C(t)$と思って解を探す方法でした。臨界減衰でこの考え方を使いましたが、計算するとこれも無理です。

　他にないのか…ということで$e^{-\lambda{t}}$だけではなく、$e^{+\lambda{t}}$と組み合わせた関数の「双曲線関数(ハイパボリック関数)」を使ってみます。定義は、

$$\tanh{(\lambda{t})}=\frac{e^{+\lambda{t}}-e^{-\lambda{t}}}{e^{+\lambda{t}}+e^{-\lambda{t}}}=\frac{\sinh{(\lambda{t})}}{\cosh{(\lambda{t})}}$$

です。$t→\infty$とすると$+1$へ収束するので、今回の最終的に速度が一定値になる現象の記述と相性が良さそうです。

実際に、この関数 $\tanh(\lambda{t})$ が解になるのか確かめてみましょう。時間$t$で微分すると、

$${\frac{d}{dt}}(\tanh(\lambda{t}))=\{1-\tanh^2(\lambda{t})\}\times\lambda$$

となります。先ほどの運動方程式の両辺を$m$で割ったもの:

$$\frac{dv}{dt}=-g+\frac{\kappa}{m}v^2=\bigg\{1-\frac{\kappa}{mg}v^2\bigg\}\times(-g)$$

と見比べると同じ構造をしていることがわかります。つまり、終端速度$v_{\infty}=-\sqrt{{mg}/{\kappa}}$に符号を合わせて２乗を外すと、

$$\bigg(\sqrt{\frac{\kappa}{mg}}v\bigg)^2=\{\tanh(\lambda{t})\}^2$$

$$\therefore{v(t)=-\sqrt{\frac{mg}{\kappa}}}\tanh(\lambda{t})$$

となります。さらに、これを微分した

と、運動方程式の両辺を$m$で割った式を見比べて、$\lambda$を求めると、

$$-\sqrt{\frac{mg}{\kappa}}\times\lambda=-g\ \ \therefore\lambda=\sqrt{\frac{\kappa{g}}{m}}$$

以上より、求めたい速度$v(t)$は、

となります。

　ここで、$\lambda=\sqrt{\kappa{g}/m}$の意味を定性的に確認しておきましょう。今度は分母に質量$m$が入っています。$\lambda$は、この$\tanh$関数がどれだけ$+1$へ近づくのか？の速さを決めています。つまり、$\lambda$が大きければ、それだけ早く収束するわけです。一方、質量$m$の意味を考えると、これは運動の変化のしにくさを表す量なので、$m$が大きくなると$\lambda$は小さくなります。したがって、分母に$m$が入ります。

実際に運動方程式を解いてみよう(変数分離法を使って)

　今度は、変数分離法を使って運動方程式:

$$m\frac{{d}{v}}{{d}{t}}=-mg+\kappa{v}^2$$

を解きます。$\tanh$の解を仮定せずに解いてみます。この微分方程式がすぐに解けない理由の１つは、２乗の項$v^2$が入っていることにあります。ところが運動方程式の右辺は$a^2-b^2$の因数分解が使えそうな形が入っています。これを利用して、実は変数分離法で解くこともできます。

　左辺に「$v$に関する項」を、右辺に「$t$に関する項」を集めてみます。まずは、右辺を$-\kappa$で括ります。

準備が整ったので、変数を分離します:

$$\frac{m}{\kappa}{}\frac{1}{{(\sqrt{mg/\kappa}\ )}^2-v^2}dv=-dt$$

ここで、部分分数分解:

$$\frac{1}{a^2-b^2}=\frac{1}{2a}\bigg(\frac{1}{a+b}+\frac{1}{a-b}\bigg)$$

を利用すると、$v^2$が分解されて積分ができるようになります。($a$ではなく、$b$が変数$v$に対応することに注意してください。もし$a$を変数$v$だと思うと、係数$1/2a$も変数になってしまうので、積分どころではなくなります。)

これの両辺を初期条件の時刻$t=0$から任意の時刻$t$まで積分すれば、求めたい$v(t)$を知ることができます。

実際に両辺を積分してみます。左辺は分数関数の積分で、右辺は定数$-1$の積分です。これは不定積分なので、積分定数$C$が付きます。さらに、$-v$の方の分数は積分して前にマイナスがつくことにも注意してください。

積分定数$C$はせっかく書きましたが、$t=0$の時に$C=0$となるのですぐに消えます。この式を整理すると、

$$\ln\bigg|\frac{\sqrt{m{g}/\kappa}+v}{\sqrt{m{g}/\kappa}-v}\bigg|=-2\sqrt{\frac{\kappa{g}}{m}}t$$

絶対値を外すことを考えます。速度$v$は、初速$0$で、どんどんとマイナスの値になり、最終的に終端速度$v_{\infty}=-\sqrt{mg/\kappa}$に達するのでした。つまり、$-\sqrt{mg/\kappa}\leq{v(t)}\leq0$が成り立ちます。したがって、

$$\sqrt{mg/\kappa}+v\geq0$$

$$\sqrt{mg/\kappa}-v\geq0$$

であるので、素直に絶対値が外せます。つまり、

$$\ln\frac{\sqrt{m{g}/\kappa}+v}{\sqrt{m{g}/\kappa}-v}=-2\sqrt{\frac{\kappa{g}}{m}}t$$

さらに、対数関数は、指数関数の逆関数なので、次のようにも書けます。

$$\frac{\sqrt{m{g}/\kappa}+v}{\sqrt{m{g}/\kappa}-v}=e^{-2\sqrt{({\kappa{g}}/{m})\ }t}$$

あと少しです。求めたいのは$v(t)$の関数形なので、左辺の分数を解消してから$v(t)$について解きます。

$${\sqrt{m{g}/\kappa}+v(t)}=({{\sqrt{m{g}/\kappa}-v(t)}})e^{-2\sqrt{({\kappa{g}}/{m})\ }t}$$

$${\therefore}(1+e^{-2\sqrt{(\frac{\kappa{g}}{m})\ }t})v(t)=-\sqrt{mg/\kappa}(1-e^{-2\sqrt{(\frac{\kappa{g}}{m})\ }t})$$

$${\therefore\ }v(t)=-\sqrt{\frac{mg}{\kappa}}\frac{1-e^{-2\sqrt{({\kappa{g}}/{m})\ }t}}{1+e^{-2\sqrt{({\kappa{g}}/{m})\ }t}}$$

$t→\infty$で、$v→v_{\infty}$となることもチェックしておきましょう。また、グラフを描く必要があれば、$t=0$で$v=0$、$t→\infty$で$v→v_{\infty}$となるように滑らかに繋げばokでしょう。

　これで一応終わりですが、穴埋め形式の試験問題の場合、意地悪されることが考えられます。分子分母に$e^{+\sqrt{({\kappa{g}}/{m})\ }t}=e^{+\theta}$を掛けて見た目を変えられるかもしれません:

$$\frac{1-e^{-2\theta}}{1+e^{-2\theta}}=\frac{e^{+\theta}-e^{-\theta}}{e^{+\theta}+e^{-\theta}}=\frac{e^{+2\theta}-1}{e^{+2\theta}+1}$$

この真ん中が双曲線関数$\tanh(\theta)$の定義ですね。