基底と座標と基底変換行列【例題付き】

ベクトル空間 $V$ に入っている元の中で、いくつか、特別な性質をもった元があります。それには「基底」という名前が与えられています。基底が特別扱いされるのには、「ベクトル空間 $V$ に入っているあらゆる元を基底の一次結合で表現できる」「基底は一次独立」という２つの理由があります。

また、与えられたベクトル空間 $V$ に対して、基底の個数(次元)は一意的に決まります。基底の個数を守れば、基底は複数通りの選び方ができて、それらの基底たちは互いに基底変換行列 $P$ で結ばれます。

基底と座標

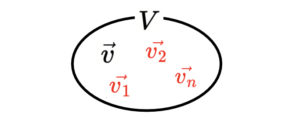
ベクトル空間 $V$ にたくさんの元が乗っています。今、ベクトル空間 $V$ の基底に

$$\mathcal{A}=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})$$

をとります。基底は $V$ の元の中でも注目すべき元なので、赤色を付けておきました。$V$ のどんな元も、基底の一次結合で表すことができて、元 $\vec{v}$は、

$$\vec{v}={c_1{\textcolor{red}{\vec{v_1}}}}+{c_2{\textcolor{red}{\vec{v_2}}}}+\cdots+{c_n{\textcolor{red}{\vec{v_n}}}}\\\ \\=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})\begin{pmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{pmatrix}$$

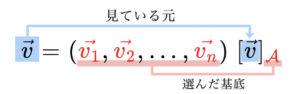
と書くことができます。ここで、基底の係数 $c_1,$ $c_2,$ $\ldots,$ $c_n$ を縦に並べたベクトルを、基底 $\mathcal{A}$ に関する $\vec{v}$ の座標と言い、$[\vec{v}]_{\mathcal{A}}$と書きます。したがって、

$$\vec{v}=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})\ [\vec{v}]_{\mathcal{A}}$$

となります。イメージとしてはこんな感じです:

ここまでをまとめます。

上で述べた通り、基底になれる元の個数は決まっていますが、基底の選び方は自由です。なので、同じ $\vec{v}$ を別な基底 $\mathcal{A}^{\prime}$ から見ることもできます。それぞれの基底に関する座標 $[\vec{v}]_{{\mathcal{A}}},$ $[\vec{v}]_{\mathcal{A}^{\prime}}$ の間には何か関係はあるのでしょうか？

基底変換行列　基底を変換する行列

ベクトル空間 $V$ の基底を２つ用意します。１つ目の基底を、

$$\mathcal{A}=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})$$

とします。もう片方の基底は、これと区別するために「 $^{\prime}$ 」を付けて、

$$\mathcal{A}^{\prime}=(\textcolor{blue}{\vec{v_1}^{\prime}},\textcolor{blue}{\vec{v_2}^{\prime}},\ldots,\textcolor{blue}{\vec{v_n}^{\prime}})$$

とします。こちらは青色にしましょう。

$\mathcal{A}$ と $\mathcal{A}^{\prime}$ どちらの基底も、同じベクトル空間 $V$ に乗っているので、一方の基底を、もう片方の基底を使って書くことができます。例えば $\textcolor{blue}{\vec{v_1}^{\prime}}$ なら、

$$\textcolor{blue}{\vec{v_1}^{\prime}}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ [\textcolor{blue}{\vec{v_1}^{\prime}}]_{\mathcal{A}}$$

と書けます。同様に $\mathcal{A}^{\prime}$ の残りの基底も $\mathcal{A}$の基底を使って書いてみましょう。

$$\textcolor{blue}{\vec{v_2}^{\prime}}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ [\textcolor{blue}{\vec{v_2}^{\prime}}]_{\mathcal{A}}\\\vdots\\\textcolor{blue}{\vec{v_n}^{\prime}}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ [\textcolor{blue}{\vec{v_n}^{\prime}}]_{\mathcal{A}}$$

これらの書き換えを $\textcolor{blue}{\vec{v_1}^{\prime}}$ から $\textcolor{blue}{\vec{v_n}^{\prime}}$ まで並べます。 $(\textcolor{red}{\vec{v_1}},$ $\textcolor{red}{\vec{v_2}},$ $\ldots,$ $\textcolor{red}{\vec{v_n}})$ の部分は共通しているので括っておきます。

$$(\textcolor{blue}{\vec{v_1}^{\prime}},\textcolor{blue}{\vec{v_2}^{\prime}},\ldots,\textcolor{blue}{\vec{v_n}^{\prime}})\\\ \\=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ \bigg[[\textcolor{blue}{\vec{v_1}^{\prime}}]_{\mathcal{A}}, [\textcolor{blue}{\vec{v_2}^{\prime}}]_{\mathcal{A}}, \ldots, [\textcolor{blue}{\vec{v_n}^{\prime}}]_{\mathcal{A}}\bigg]\ (*)$$

綺麗にまとまりました。この式の、大きな括弧の部分 $[\cdots]$ は、列ベクトルである「座標」を横に並べた成分から構成されているので、行列になっています。この部分を、

$$P=\bigg[[\textcolor{blue}{\vec{v_1}^{\prime}}]_{\mathcal{A}}, [\textcolor{blue}{\vec{v_2}^{\prime}}]_{\mathcal{A}}, \ldots, [\textcolor{blue}{\vec{v_n}^{\prime}}]_{\mathcal{A}}\bigg]$$

として、行列 $P$ と呼ぶことにします。すると、先程の $(*)$ 式は、次のようになります:

$$\underbrace{(\textcolor{blue}{\vec{v_1}^{\prime}},\textcolor{blue}{\vec{v_2}^{\prime}},\ldots,\textcolor{blue}{\vec{v_n}^{\prime}})}_{\mathcal{A}^{\prime}}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})}_{\mathcal{A}}\ P$$

ついに $\mathcal{A}$ と $\mathcal{A}^{\prime}$ の関係が見えました！ $P$ という行列を、基底 $\mathcal{A}$ の並びに右から掛けると、基底 $\mathcal{A}^{\prime}$ の並びに変わる、と読むことができます。このような行列 $P$ を、

$\mathcal{A}$から$\mathcal{A}^{\prime}$への基底変換行列

と言います。このような行列を右から掛けることにより、文字通り、基底を変換することができます。

次に、ベクトル空間 $V$ の適当な元 $\vec{v}$ を持ってきます。 基底ではない場合もあるので、文字色は黒のままで行きます。この元を基底 $\mathcal{A}^{\prime}$ を使って書くと、

$$\vec{v}=\underbrace{(\textcolor{blue}{\vec{v_1}^{\prime}},\textcolor{blue}{\vec{v_2}^{\prime}},\ldots,\textcolor{blue}{\vec{v_n}^{\prime}})}_{\mathcal{A}^{\prime}}\ [\vec{v}]_{\textcolor{blue}{\mathcal{A}^{\prime}}}$$

となります。さて、上で登場した$\mathcal{A}$から$\mathcal{A}^{\prime}$への基底変換行列 $P$ を使えば、$\mathcal{A}$の基底に変えることができます。 $\underbrace{(\cdots)}_{\mathcal{A}^{\prime}}$ の部分を書き換えると、

$$\vec{v}=\underbrace{(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})\ P}_{=(\textcolor{blue}{\vec{v_1}^{\prime}},\textcolor{blue}{\vec{v_2}^{\prime}},\ldots,\textcolor{blue}{\vec{v_n}^{\prime}})}\ [\vec{v}]_{\textcolor{blue}{\mathcal{A}^{\prime}}}$$

となりました。ところで、 $\vec{v}$ を基底 $\mathcal{A}$ を使って書くと、

$$\vec{v}=(\textcolor{red}{\vec{v_1}},\textcolor{red}{\vec{v_2}},\ldots,\textcolor{red}{\vec{v_n}})\ [\vec{v}]_{\textcolor{red}{\mathcal{A}}}$$

でした。元は、同一の基底を用いると一次結合でただ一通りに表せるので、

$$P\ [\vec{v}]_{\textcolor{blue}{\mathcal{A}^{\prime}}}=[\vec{v}]_{\textcolor{red}{\mathcal{A}}}$$

という座標の関係が得られます。座標は列ベクトルなので、この関係式は、$\mathcal{A}^{\prime}$に関する座標を$\mathcal{A}$に関する座標へ変換する式、と読むことができます。図で描くと次のようになります。

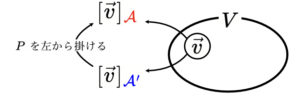
以上の内容をまとめます。

基底変換行列についての例題

基底変換行列 $P$ は、同一のベクトル空間 $\mathbb{R}^3$ に乗った基底 $\mathcal{A}, \mathcal{B}$ を結ぶのが役割です。これを式として書くと、

$$(\vec{b}_1, \vec{b}_2, \vec{b}_3)=(\vec{a}_1, \vec{a}_2, \vec{a}_3)\ P$$

となり、基底 $\mathcal{A}$ に行列 $P$ を右からかけることによって、基底 $\mathcal{B}$ へと変換されています。この式の $P$ を求めるのがこの問題です。２種類の方法で解いてみました→「 $A$の逆行列を使って求める」「 ダイレクトに求める」

$A$の逆行列を使って求める

ここからは、$A=(\vec{a}_1, \vec{a}_2, \vec{a}_3), $ $B=(\vec{b}_1, \vec{b}_2, \vec{b}_3)$ と置きます。すると、これらは行列 $P$ を使って

$$B=AP$$

のように結ばれます。ここで、行列 $A$ は基底で構成されていて、それゆえ $\vec{a}_1, \vec{a}_2, \vec{a}_3$ は一次独立なので、行列 $A$ は正則であり、逆行列 $A^{-1}$ を持ちます。(ここは「 行列の正則と一次独立 」が参考になると思います。)

したがって、両辺に左から $A^{-1}$ を掛けることで、

$$A^{-1}B=P$$

と変形でき、結局、$A$ の逆行列を $B$ に掛ければ $P$ を求めることができます。ところで逆行列 $A^{-1}$ は、「行列 $A$ から単位行列 $E$ を作る行基本変形」と同じ変形を単位行列 $E$ に施すことで得ることができます。この場合は、左側に $A$ を、右側に $E$ を配置した行列を簡約化していけば良いわけです。

$$\left[\begin{array}{ccc|ccc}2&1&0&1&0&0\\0&1&-1&0&1&0\\1&0&1&0&0&1\end{array}\right]→\cdots→\\\ \\\left[\begin{array}{ccc|ccc}1&0&0&1&-1&-1\\0&1&0&-1&2&2\\0&0&1&-1&1&2\end{array}\right]\\ \ \\\therefore{A^{-1}=}\left[\begin{array}{ccc}1&-1&-1\\{-1}&2&2\\{-1}&1&2\end{array}\right]$$

これより、$A^{-1}$ を求めることができました。次に、$P=A^{-1}B$ なので、$B$ にこれを掛ければ $P$ が求まります。

$$P=A^{-1}B=\cdots=\left[\begin{array}{ccc}0&1&0\\1&0&0\\2&-2&-1\end{array}\right]$$

この方法は二度手間ですね。少し工夫したのが次の考え方です。

ダイレクトに求める($A$ が正則でない場合も)

直接 $A^{-1}B$ を求めてしまおう、というのがこちらの方法です。$A$ の逆行列を求める過程を思い出すと、$A$ を $E$ にする行基本変形を、$E$ に施すと $A^{-1}$ になる、というものでした。これはつまり、

$$\left[\begin{array}{c|c}\textcolor{red}{A}&E\end{array}\right]→\cdots→\left[\begin{array}{c|c}\textcolor{red}{E}&A^{-1}\end{array}\right]$$

と書けるわけですが、この変形を行う前に、この行列の右側に $B$ を掛けておけば一発で求めることができます。つまり、

$$\left[\begin{array}{c|c}\textcolor{red}{A}&\textcolor{blue}{B}\end{array}\right]→\cdots→\left[\begin{array}{c|c}\textcolor{red}{E}&A^{-1}\textcolor{blue}{B}\end{array}\right]\\\ \\=\left[\begin{array}{c|c}\textcolor{red}{E}&P\end{array}\right]$$

$A$ を単位行列 $E$ にするような行基本変形(すなわち $A^{-1}$ を左からかけること)を、同時に $B$ にもやってあげるわけです。

実際にこの問題でも計算してみると、

$$\left[\begin{array}{ccc|ccc}2&1&0&1&2&0\\0&1&-1&-1&2&1\\1&0&1&2&-1&-1\end{array}\right]→\cdots\\\ \\→\left[\begin{array}{ccc|ccc}1&0&0&0&1&0\\0&1&0&1&0&0\\0&0&1&2&−2&−1\end{array}\right]$$

のように求めることができます。

表現行列へ続く…　↓

2021年1月24日表現行列【例題付き】